书名：算法分析导论（第2版）
ISBN：978-7-115-62661-5
本书由人民邮电出版社发行数字版。版权所有，侵权必究。
您购买的人民邮电出版社电子书仅供您个人使用，未经授权，不得以任何方式复制和传播本书内容。
我们愿意相信读者具有这样的良知和觉悟，与我们共同保护知识产权。
如果购买者有侵权行为，我们可能对该用户实施包括但不限于关闭该帐号等维权措施，并可能追究法律责任。
著 [美] 罗伯特·塞奇威克（Robert Sedgewick） [法] 费利佩·弗拉若莱（Philippe Flajolet）
译 常 青 左 飞
责任编辑 杨绣国
人民邮电出版社出版发行 北京市丰台区成寿寺路11号
邮编 100164 电子邮件 315@ptpress.com.cn
网址 http://www.ptpress.com.cn
读者服务热线：(010)81055410
反盗版热线：(010)81055315
本书全面介绍了算法的数学分析所涉及的主要技术，涵盖的内容来自经典的数学课题（包括离散数学、初等实分析和组合数学等），以及经典的计算机科学课题（包括算法和数据结构等）。本书的重点是平均情况或概率性分析，书中也论述了最差情况或复杂性分析所需的基本数学工具。本书第1版为行业代表性著作，第2版不仅对书中图片和代码进行了更新，还补充了新章节。全书共9章，第1章介绍算法分析；第2～5章介绍数学方法；第6～9章介绍组合结构及其在算法分析中的应用。
本书适合作为高等院校数学、计算机科学以及相关专业的本科生和研究生的教材，也可供相关技术人员和爱好者学习参考。
2014年的冬天，一部讲述“计算机科学之父”艾伦·图灵（Alan Turing）传奇人生的传记电影在美国上映，这部影片就是《模仿游戏》。次年，该片荣获第87届奥斯卡金像奖最佳改编剧本奖，以及包括最佳影片、最佳导演、最佳男主角、最佳女配角在内的7项提名，一时风光无限。
图灵一生最重要的三大贡献包括图灵机、图灵测试以及破译Enigma密码，其中的每一项都值得全世界感谢和纪念他。在提出图灵测试的论文中，图灵石破天惊地预言了创造出具有真正智能的机器的可能性，这也是人工智能研究的源头。事实上，《模仿游戏》这个名字正是图灵那篇著名论文第1章的标题。后人为了纪念图灵对计算机科学所做出的巨大贡献，将该领域的最高奖命名为“图灵奖”。而破译Enigma密码更是直接帮助盟军在战场上取得了先机，拯救了无数人的性命并最终取得第二次世界大战反法西斯阵营的全面胜利。
尽管前面提到的两大贡献已是功若丘山，但笔者这里将从图灵的另外一个贡献——图灵机谈起，因为这与本书所要讨论的话题息息相关。为此，我们还得把时间再往前推。1900年，德国数学家大卫·希尔伯特（David Hilbert）在国际数学家大会上做了题为《数学问题》的演讲，提出了著名的希尔伯特之23个问题。尽管此后的数学发展远远超过了希尔伯特的预料，但他所提出的这23个问题仍然对20世纪的数学发展起到了重要的推动作用。
希尔伯特的第10个问题是要设计一个算法来测试多项式是否有整数根。他没有使用“算法”这个术语，而是采用了下面这种表述：“通过有限多次运算就可以决定的过程。”有意思的是，从希尔伯特对这个问题的陈述中可以看出，他明确地要求设计一个算法。因此，显然他假设这样的算法是存在的，人们所要做的只是找到它。现在我们知道，这个任务是无法完成的，即它是算法上不可解的。但对那个时期的数学家来说，以他们对算法的直观认识，得出这样的结论是不可能的。
非形式地说，算法是为实现某个任务而构造的简单指令集。用日常用语来说，算法又被称为过程或者方法。算法在数学中也起着非常重要的作用。古代数学资料中就包含执行各种各样计算任务的算法描述。例如，我国古代数学经典《九章算术》中就记述了包括求最大公约数、求最小公倍数、开平方根、开立方根等在内的诸多算法。
虽然算法在数学中已有很长的历史，但在20世纪之前，算法本身一直没有精确的定义。数学家面对希尔伯特的第10个问题束手无策。由于缺乏对算法本身的精确定义，要证明某个特定任务不存在算法就更不可能了。要想破解希尔伯特的第10个问题，人们不得不等待算法的精确定义出现。
直到1936年，曙光似乎出现了。图灵向伦敦的权威数学杂志递交了一篇题为《论数字计算在决断难题中的应用》的论文。该文最终于1937年正式发表，并立即引起了广泛关注。在论文中，图灵描述了一种可以辅助数学研究的机器，也就是后来被称为“图灵机”的抽象系统。与此同时，另外一位数学家阿隆佐·丘奇（Alonzo Church）也独立地提出了另外一套系统，即所谓的Lambda演算。图灵采用他的图灵机来定义算法，而丘奇则采用Lambda演算来定义算法，后来图灵证明这两个定义是等价的。由此，人们在算法的非形式概念和精确定义之间建立了联系，即算法的直觉概念等价于图灵机，这就是所谓的“丘奇－图灵”论题。
“丘奇－图灵”论题提出的算法定义是解决希尔伯特第10个问题所需的，而第10个问题的真正解决则直到1970年，借助于丘奇与图灵的杰出贡献，卡里·马提亚塞维齐（Yuri Matiyasevich）在马丁·戴维斯（Martin Davis）、希拉里·普特纳姆（Hilary Putnam）和朱莉娅·罗宾逊（Julia Robinson）等人工作的基础上，最终证明检查多项式是否有整数根的算法是不存在的。上述四人的名字也紧紧地同希尔伯特的第10个问题联系在了一起。破解希尔伯特的第10个问题的过程更像一场声势浩大又旷日持久的国际协作和学术接力。每个人的工作都必不可少，而且大家都感觉已经相当接近问题的最终答案。历史见证了马提亚塞维齐敏锐地接过最后一棒并完成终点冲刺的伟大一幕。更有意思的是，彼时正值美苏冷战最为紧张的时期，两个超级大国之间的正常学术交流几乎完全中断。但这或许就是科学无国界的一个重要体现，尽管国家层面上双方剑拔弩张，而科学家在私下仍然以一种惺惺相惜的默契方式彼此神交。特别是在得知苏联数学家完成了最终的证明时，美国同行都相当振奋和由衷地喜悦，这不得不说是学术界的一段佳话。
回顾建立算法形式化定义和破解希尔伯特第10个问题的那段风起云涌的历史，我们不得不由衷地感叹：算法对于我们的世界是多么重要。可以这样说，自计算机科学诞生之日起，关于算法的研究就一直是一个核心话题。现代计算机科学中充满了各种各样的算法，许多图灵奖得主也正是因提出的各种经典算法而闻名于世。例如，提出单源最短路径算法的艾兹格·迪科斯彻（Edsger Dijkstra）[1]、提出字符串匹配算法的唐纳德·E.克努特，中文名为高德纳（Donald E.Knuth）[2]、提出多源最短路径算法的罗伯特·弗洛伊德（Robert Floyd）[3]，以及提出快速排序算法的安东尼·霍尔（Antony Hoare）[4]等。其中，高德纳是最年轻的图灵奖得主这一纪录的保持者（获奖时年仅36岁），并以计算机算法设计与分析领域的经典巨著《计算机程序设计艺术》而广为人知。
[1] 1972年图灵奖得主。
[2] 1974年图灵奖得主。
[3] 1978年图灵奖得主。
[4] 1980年图灵奖得主。
作为导师，高德纳一生共指导过28位博士生，而本书作者之一的罗伯特·塞奇威克（Robert Sedgewick）便是其中之一。塞奇威克是普林斯顿大学计算机科学系的创立者暨首任系主任，还是著名的Adobe公司的董事。作为一位世界知名的计算机科学家，塞奇威克于1997年当选ACM（Association for Computing Machinery，国际计算机学会）会士，并因从对称二叉树中导出了红黑树而享誉计算机界。
塞奇威克与费利佩·弗拉若莱（Philippe Flajolet）曾合作撰写过数本算法分析领域的著作，本书即为其中一部在全世界范围内广泛流传的经典之作。弗拉若莱是法国计算机科学家、法国科学院院士，被称为“分析组合学之父”。他与合作者共同提出的Flajolet-Martin算法更是当今互联网与大数据时代背景下，网站分析统计的重要基石。
然而，天妒英才，2011年3月，弗拉若莱突然离世。悲痛万分的塞奇威克怀着对逝者的无限缅怀写了感人至深的悼词：“弗拉若莱的离世意味着很多秘密再也无法揭开。但他给世人留下了很多追随他脚步的继承者，我们会继续追寻他的数学梦想。”在这样的背景下，塞奇威克以极大的热情投入工作，历经数百个日夜，终于在2012年10月将本书的第2版付梓。塞奇威克坚信弗拉若莱的精神会在后人的工作中得到永生，进而希冀本书的读者能够循着弗拉若莱的脚步，继续追求他的数学梦想。
本书全面系统地介绍了算法分析中需要使用的基本技术，所涉及的内容既有来自包括离散数学、初等实分析、组合数学等在内的经典数学课题，也有来自算法及数据结构等的计算机科学课题，像递归、母函数、树、字符串、映射以及散列等算法分析话题均有讨论。可以说本书是一本研究算法分析的权威之作。
作为译者，我们希望自图灵以来的算法研究能够在更宽阔的范围内发扬光大，尤其希望中国的计算机科研人员能够从本书中找到启迪研究工作的智慧。同时，希望通过本书向神交已久的两位大师——塞奇威克和弗拉若莱送上最崇高的敬意。
最后，本书翻译工作的完成有赖于数位合作者的倾心付出，其中常青翻译了本书的第1至6章，左飞翻译了第8、9章，于佳平翻译了第7章。其他参与本书翻译和校对工作的人员还有李振坡、邵臣、叶剑、赵冰冰、贾啸天、钱文秀、丁星芸、李晓华、黄帅。自知论道须思量，几度无眠一文章。因时间和水平有限，纰漏与不足之处在所难免，译者恳切地期望广大同行及读者朋友不吝批评斧正。
分析算法可以给人带来两方面的快乐。其一，人们可以尽享优雅计算过程中所蕴含的让人沉醉的数学模式；其二，我们所学到的理论知识可以让自己更好更快地完成工作，这无疑是最实际的好处。
尽管数学模型只是对真实世界的一种理想化近似，但它对所有的科学活动而言都可谓是一剂灵丹妙药。在计算机科学中，数学模型往往可以精确地描述计算机程序所创造的世界，数学模型的重要性也因此大大增加了。我想，这也是为什么我在读研究生时会沉迷于算法分析，以至于这成为迄今为止我的主要工作。
但直到今天，算法分析在很大程度上还是局限在相关专业的研究生和科研人员的圈子里。算法分析的概念既不晦涩也不复杂，但确实比较新，所以相关概念的学习和使用都还需要一些时间才能成熟。
现在，经过40余年的发展，算法分析已经非常成熟，足以成为计算机专业标准课程中的一部分。塞奇威克和弗拉若莱写的这本众人翘首以盼的教科书也因此备受欢迎。塞奇威克和弗拉若莱不仅是算法分析领域的专家，也是算法分析的布道大师。我坚信，每一位细细品读这本书的计算机研究人员都会从中获益。
唐纳德·E.克努特（Donald E. Knuth）
本书的主要目的是介绍算法的数学分析中涉及的主要技术，涵盖的内容来自经典的数学和计算机科学领域，包括来自数学领域的离散数学、初等实分析和组合数学，来自计算机科学领域的算法和数据结构等。本书的重点是平均情况或概率性分析，对最差情况或复杂性分析所需的基本数学工具也有所涉及。
我们假设读者对计算机科学和实分析的基本概念是比较熟悉的。简单来说，读者要能够编写程序和证明定理。除此之外，本书对读者没有其他要求。
本书主要用作高阶算法分析课程的教科书。书中涵盖了计算机专业学生所需离散数学的基本技术、组合学和重要离散结构的基本属性等内容，因此本书也可以用在计算机专业的离散数学课程中。通常此类课程所涵盖的内容都比较广泛，很多教师会用自己的方法来选取其中的一部分内容教给学生，因此本书还可以用于给数学和应用数学专业的学生介绍计算机科学中与算法和数据结构有关的基本原理。
关于算法的数学分析的论文非常多，但这个领域的学生和研究人员却很难学习到该领域中广泛使用的方法和模型。本书的目标就是解决这个问题，一方面要让读者知道这个领域所面临的挑战，另一方面要让读者有足够的背景支持来学习为应对这些挑战而正在开发的工具。我们列出了相关的参考资料，因此本书可以作为研究生算法分析入门课程的基础教材，也可以用作想学习该领域中相关资料的数学和计算机科学领域研究人员的参考资料。
如读者有大学一二年级或与之同等的数学基础，学习过组合学和离散数学，以及实分析、数值方法和基本数论方面的课程，将有助于理解本书中的内容（有些内容跟本书是交叉的）。本书虽会涉及这些领域，但只会对必要的内容做介绍。我们会列出参考资料供想进一步学习的读者参考。
读者需要拥有一到两个学期大学水平的编程经验，包括了解基本数据结构。我们不会涉及编程和具体实现的问题，但算法和数据结构是我们的核心。同数学方面的基础知识一样，在本书中我们会简要介绍基本的信息，同时列出标准教材和知识来源供读者参考。
与本书有关的图书包括唐纳德·E.克努特写的《计算机程序设计艺术》（The Art of Computer Programming），塞奇威克和韦恩（Wayne）写的《算法（第4版）》（Algorithms, Fourth Edition），科门（Cormen）、莱瑟森（Leiserson）、里维斯特（Rivest）和斯坦（Stein）写的《算法导论》（Introduction to Algorithms），以及我们自己写的《分析组合论》（Analytic Combinatorics）。本书可以作为这些书的补充材料。
从基本思路上来说，本书与唐纳德·E.克努特的书是最相似的。但本书的重点是算法分析中的数学技术，而唐纳德·E.克努特的那些书是内容更丰富的百科全书，其中算法的各种性质是主角，算法分析方法只是配角。本书可以作为学习唐纳德·E.克努特书中进阶内容的基础。本书还涵盖了唐纳德·E.克努特的书诞生之后在算法分析领域出现的新方法和新成果。
本书尽可能地涵盖各种重要、有趣的基础算法，例如，塞奇威克和韦恩的《算法（第4版）》中所介绍的那些算法。《算法》一书涵盖了经典的排序、搜索和用于处理图和字符串的算法，本书的重点是介绍用于预测算法性能和比较算法性能优劣的数学知识。
科门（Cormen）、莱瑟森（Leiserson）、里维斯特（Rivest）和斯坦（Stein）合著的《算法导论》是算法方面的标准教材，其中提供了关于算法设计的各种资料。《算法导论》一书（及相关的资料）关注的是算法设计和理论，大部分是基于最差性能边界的。而本书关注的则是算法分析，尤其是各种科学研究（而不是理论研究）所需的技术。第1章就是为此做铺垫的。
本书还会介绍分析组合学，它可以让读者开阔视野，也有助于开发用于新研究的高级方法和模型，而且不局限于算法分析，它还可以用于组合学和更广泛的科学应用。那一部分对读者的数学水平要求更高一些，差不多需要本科高年级学生或研究生一年级学生的水平。当然，仔细阅读本书也有助于读者学习相关的数学知识。我们的目标是尽可能让读者感兴趣，有动力进行更深入的学习。
本书读者在数学和计算机科学方面的知识储备肯定是不一样的。所以，读者要注意本书的结构：全书共9章，第1章是导论，介绍算法分析，第2～5章介绍数学方法，最后的4章是组合结构及其在算法分析中的应用。具体如下：
导论
第1章 算法分析
数学方法
第2章 递归关系
第3章 母函数
第4章 渐近逼近
第5章 分析组合
组合结构及其在算法分析中的应用
第6章 树
第7章 排列
第8章 字符串与字典树
第9章 单词与映射
第1章介绍全书的主要内容，帮助读者理解本书的基本目标以及其余各章的目的。第2～4章涵盖了离散数学中的方法，重点是基本概念和技术。第5章是一个转折点，其中涵盖了分析组合学的内容。计算机和计算模型的出现带来了很多新问题，这些问题往往涉及大型的离散结构。分析组合学就是研究这些离散结构以解决新出现的问题的。第6～9章则回到了计算机科学，内容涵盖了各种组合结构的属性、它们与基本算法的关系以及分析结果。
我们试图让本书是自包含的，本书的组织结构可以让教师很方便地根据学生和教师自己的背景及经验选取要重点讲解的部分。一种比较偏数学的教学方案是重点讲解本书第2～5章的理论和证明，然后过渡到第6～9章的相关应用。另一种比较偏计算机科学的方案是简要介绍第2～5章的数学工具，将重点放在第6～9章与算法有关的内容上。但我们的根本目标还是要让绝大部分的学生能通过本书学习到数学和计算机科学的新知识。
本书还罗列了很多参考资料以及数百个习题，鼓励读者去研究原始材料，以便更深入地研究本书中的内容。根据我们的教学经验，教师可以通过计算实验室和家庭作业，灵活地组织授课和阅读材料。本书的内容为学生深入学习诸如Mathematica、Maple或Sage之类的符号计算系统提供了一个很好的框架。更重要的是，对学生而言，通过比较数学研究结果和实际测试结果得出的结论是有重要价值的，不可忽略。
本书的一个重要特点就是拥有配套的网站aofa.cs.princeton.edu。这个网站是免费的，提供了很多关于算法分析的补充材料，包括课件和相关网站的链接，其中有一些关于算法和分析组合学的网站。这些材料对讲授这些内容的教师和自学者都很有帮助。
我们非常感谢普林斯顿大学、INRIA和NSF（美国国家科学基金会），它们是我们这本书的主要资助者。其他的资助来自布朗大学、欧洲共同体（Alcom项目）、美国国防分析研究院、法国研究与技术部、斯坦福大学、布鲁塞尔自由大学和施乐帕克研究中心。本书历时多年才得以付梓，在此不可能一一列出为本书提供支持和帮助的人和机构，我们对此深表歉意。
正如书中所说，唐纳德·E.克努特对本书有重要的影响。
过去几年，在普林斯顿、巴黎和普罗维登斯听过我们讲课的学生们为本书提供了宝贵的反馈意见。全世界各地的学生和教师也为本书的第1版提出了很多好建议。在此特别感谢菲利普·杜马斯（Philippe Dumas）、摩德凯·戈林（Mordecai Golin）、赫尔穆特·普罗丁格（Helmut Prodinger）、米歇尔·索里亚（Michele Soria）、马克·丹尼尔·沃德（Mark Daniel Ward）和马克·威尔逊（Mark Wilson）的帮助。
弗利佩·弗拉若莱和罗伯特·塞奇威克 1995年9月于科孚岛
罗伯特·塞奇威克 2012年12月于巴黎
2011年3月，我和我的妻子琳达（Linda）去了一个美丽而遥远的地方旅行，因此有几天没上网。当我找到机会处理邮件时，却得到一个让人震惊的消息：我的挚友和同事弗拉若莱突然去世了。由于无法及时赶到巴黎参加葬礼，我和琳达为我们的好朋友写了悼词，在此分享给本书的读者，让我们一起缅怀我们的这位朋友。
悲痛万分，我在一个遥远的地方缅怀我长期以来的好友和同事弗利佩·弗拉若莱。很遗憾不能亲自参加葬礼，但我坚信，将来一定有很多机会来缅怀弗拉若莱，希望到时我能参与。
弗拉若莱才华横溢、匠心独运、求知若渴、不知疲倦，同时慷慨大方、乐善好施，他的生活方式深深地感染了我。他改变了很多人的生活，包括我自己的。随着我们的诸多研究论文变成综述，进而发展成若干篇章、第一本书、第二本书，最终写书成为我们一生的工作——在跟弗拉若莱携手同行时，我与全世界很多学生和合作者都感受到了弗拉若莱的真诚和友好。我们曾在全世界各个地方的咖啡馆、酒吧、午餐室或客厅里一起工作。无论在何处，弗拉若莱的工作方式始终不变。我们会先聊聊某个朋友的趣事，然后开始工作。一个眼神的交流，真诚的笑声，抽两根烟，喝两口啤酒，咬两口牛排，吃点薯条，然后听到一声“好……”，我们就这样解决一个又一个问题，证明一条又一条定理。对很多与他合作过的人而言，这些时刻都铭记心中。
这个世界又少了一个聪明、高效的数学家。弗拉若莱的离世意味着很多秘密再也无法揭开。但他给世人留下了很多追随他脚步的继承者，我们会继续追寻他的数学梦想。我们会在会议上为他举杯，我们会以他的研究成果为基础继续前进，我们的论文会加上一句铭文——“谨以此纪念弗利佩·弗拉若莱”，我们会将此一代代传承下去。亲爱的朋友，我们非常想念你，我坚信，你的精神会在我们的工作中得到永生。
我和弗拉若莱合著的《算法分析导论》一书的第2版就是这样完成的。谨以此书纪念弗拉若莱，也希望更多的人通过这本书继续追寻弗拉若莱的数学梦想。
罗伯特·塞奇威克于罗得岛州詹姆斯敦
向下取整函数，或直接称为floor函数
不大于x的最大整数
向上取整函数，或直接称为ceiling函数
不小于x的最小整数
小数部分
lbN 以2为底的对数
自然对数
二项式系数
从n件物品中，不分先后地选取k件的方法总数
第一类Stirling数
拥有k个环的n个元素的排列数
第二类Stirling数
把n个元素分成k个非空子集的方法数
黄金比例
欧拉常数
Stirling常数
本书由异步社区出品，社区（https://www.epubit.com/）为您提供后续服务。
作者和编辑尽最大努力来确保书中内容的准确性，但难免会存在疏漏。欢迎您将发现的问题反馈给我们，帮助我们提升图书的质量。
当您发现错误时，请登录异步社区（https://www.epubit.com/），按书名搜索，进入本书页面，单击“发表勘误”，输入错误信息，单击“提交勘误”按钮即可（见下图）。本书的作者和编辑会对您提交的错误信息进行审核，确认并接受后，您将获赠异步社区的100积分。积分可用于在异步社区兑换优惠券、样书或奖品。
我们的联系邮箱是contact@epubit.com.cn。
如果您对本书有任何疑问或建议，请您发邮件给我们，并请在邮件标题中注明本书书名，以便我们更高效地做出反馈。
如果您有兴趣出版图书、录制教学视频，或者参与图书翻译、技术审校等工作，可以发邮件给我们。
如果您所在的学校、培训机构或企业想批量购买本书或异步社区出版的其他图书，也可以发邮件给我们。
如果您在网上发现有针对异步社区出品图书的各种形式的盗版行为，包括对图书全部或部分内容的非授权传播，请您将怀疑有侵权行为的链接通过邮件发送给我们。您的这一举动是对作者权益的保护，也是我们持续为您提供有价值的内容的动力之源。
“异步社区”是由人民邮电出版社创办的IT专业图书社区，于2015年8月上线运营，致力于优质内容的出版和分享，为读者提供高品质的学习内容，为作译者提供专业的出版服务，实现作者与读者在线交流互动，以及传统出版与数字出版的融合发展。
“异步图书”是异步社区策划出版的精品IT图书的品牌，依托于人民邮电出版社在计算机图书领域40余年的发展与积淀。
从一般性的复杂研究到特定的分析结果，对计算机算法性质的数学研究已经得到广泛应用。在本章，我们的目标是：为读者提供学习不同算法方法的视角，将我们研究的领域置于相关领域之中，并为本书的剩余部分做铺垫。为此，我们阐述了一个基础且具有代表性的问题领域概念，即排序算法的研究。
首先，我们需要思考进行算法分析的一般动机。为什么要分析一个算法？这样做有什么好处？怎样简化这个过程？然后，我们讨论算法理论，并以归并排序（Mergesort算法）作为示例，它是一种“最优”排序算法。接下来，我们以快速排序（Quicksort算法）为例，看看算法分析包含哪些方面的内容。这包括对基本快速排序算法的各种改进性研究，并通过一些示例说明算法如何帮助调整参数以提高性能。
这些示例反映了对离散数学某些领域背景的明确需要。第2章到第4章介绍了递归、母函数和渐近，这些是算法分析所需的基本数学概念。第5章介绍了符号化方法（symbolic method），这是一个将本书大部分内容联系在一起的标准化方法。第6章到第9章研究基本算法和数据结构的基本组合学特性。因为计算机科学应用的基本方法和经典数学分析之间有密切联系，所以本书同时参考了这两个领域的介绍资料。
1.1 为什么要做算法分析依据不同的参考标准，“为什么要做算法分析”这个问题有几种答案。参考标准主要有：算法的潜在应用、算法在理论与实践方面与其他算法关联的重要性、分析的难度以及所需结果的精度和准确度。
进行算法分析最直接的原因是发现算法的特点，以便评估其对各种应用的适用性；或者与同一应用的其他算法做比较。通常，我们感兴趣的是时间和空间资源，尤其是时间。简单来说，我们想知道在特定的计算机上，某一算法运行完毕究竟需要多长时间和多大空间。我们尽量使分析的结果独立于特定的运行条件——尽可能得到能够反映算法基本特点的结果，因为这样的结果可用于精确估计各种物理机器的真实资源需求量。
在实际操作中，保证算法与运行条件之间的独立性可能非常困难。因为执行的质量、编译器的性质、机器的结构以及运行环境等对算法的性能有着显著影响。为了确保分析结果是有价值的，我们必须了解这些影响因素。从另一方面来讲，在某些情况下，进行算法分析有利于该算法充分利用编程环境。
除去时间和空间资源，有时一些其他的特性也具有价值，那么分析的重点也会相应改变。例如，通过研究移动设备上的算法，可以确定其对电池寿命的影响；或者通过对数值问题算法的研究来确定所提供答案的准确度。此外，在分析中着眼于多种资源有时是正确的做法。例如，一个占用了大量内存的算法可能比占用少量内存的算法的运行时间少得多。事实上，如此仔细地进行算法分析的主要目的是：在这种情况下，为做出恰当的决策提供准确信息。
算法分析这个术语用来描述两种截然不同的通用方法，其将对计算机程序性能的研究建立在科学的基础上。下面，我们分别考虑这两种方法。
首先来看第一种方法，其推广者有Aho、Hopcroft和Ullman[2]，还有Cormen、Leiserson、Rivest和Stein[6]。该方法能够确定某一算法最劣情况下性能的增长量（“上限”）。用这种方法进行分析的主要目的是确定哪种算法的性能最佳，因为对于相同的问题，匹配下限能够证明任何算法的最坏情况的性能。我们将这种类型的分析称为算法理论（theory of algorithms）。这是计算复杂度的一种特殊情况，是问题、算法、语言和机器之间关系的一般性研究。算法理论的出现开启了设计时代，并由此针对众多关键问题开发了许多能够不断改善最坏情况性能界限的新算法。然而，为了实现这种算法的实际效用，还需要进行更加详细的分析，也许会用到本书中描述的工具。
接下来我们讨论算法分析的第二种方法，该方法的推广者是Knuth[17][18][19][20][22]。该方法能够精确表征算法在最优情况、最坏情况和平均情况下的性能，此方法中运用了一种在必要时结果的准确度能够不断提升的算法。用这种方法进行分析的主要目的是：当某一算法运行在特定计算机上时，能够精确地预测该算法的性能特点，以便预测资源利用率、参数设置和比较算法。这种类型的分析方法叫作科学（scientific）：通过构建数学模型来描述现实中算法实现的性能，然后利用这些模型进一步延伸已通过实验验证的假设。
我们可以将这两种方法视为算法设计和分析的必要步骤。当面对一个解决新问题的新算法时，我们会对这样的粗略想法感兴趣：新算法的预期表现可能如何，针对同一问题，与其他算法相比可能如何，甚至新算法有无可能是最好的。算法理论可以实现这一点。然而，在这样的分析中通常达不到足够精准。因为算法分析提供的帮助预测具体实现性能或者将两个算法进行正确比较的特定信息很少。正如我们所见，为了能够达到这样的效果，需要关于实现过程的细节、要使用的计算机以及由算法控制的结构的数学属性。算法理论可能被视为发展中更为精细、更为准确的分析过程的第一步；我们更倾向于使用算法分析这个术语来指代整个过程，其目的是提供尽可能准确的答案。
算法分析能够帮助我们更深入地理解算法，还能提供明智的改进思路。算法越复杂，分析就越困难。但是，经过算法分析，算法往往变得更简单、更精致。更重要的是，正确分析所要求的细致检查，通常使得算法能在特定计算机上更好、更有效地“实现”。分析要求对算法理解得更全面，这种理解比只是得到能够正常运行的实现方法更加深刻而全面。实际上，当分析结果和实验研究结论一致时，就能确信算法的有效性及分析过程的正确性。
有些算法是值得分析的，因为这些分析能够充实现有的数学工具。这些算法虽然可能只有有限的实际价值，但由于可能与存在实际价值的算法具有相似的属性，理解这样的算法就可能有助于以后理解更重要的算法。其他算法（有些具有很高的实际价值，有些只有很少或者没有实际价值）具备复杂的性能结构，这些结构具有独立的数学意义。动态元素通过算法分析引发的组合性问题带来了既具挑战性又有趣味的数学问题，这些数学问题扩展了经典组合学的范围，有助于揭示计算机程序的特性。
为了更清楚地表达这些思想，接下来我们首先从算法理论的角度出发，然后依循本书展开的科学观点，仔细分析一些经典结果。作为一个证明不同观点的示例，我们研究排序算法（sorting algorithms），它按照数字顺序、字母顺序或其他顺序重新排列列表。排序是一个重要的实际问题，这个问题现在仍然被广泛研究，因为它在许多应用中起到核心作用。
1.2 算法理论算法理论的主要目的是根据算法的性能特点对其进行分类。为了方便讨论，相关概念用数学符号表示如下。
定义：给定函数f(N)，则
O(f(N))表示所有g(N)的集合，当N→∞时，|g(N)/f(N)|有上界。
Ω(f(N))表示所有g(N)的集合，当N→∞时，|g(N)/f(N)|以一个（严格的）正数作为下界。
Θ(f(N))表示所有g(N)的集合，当N→∞时，|g(N)/f(N)|既有上界，又有下界。
这些符号改编自经典分析，1976年Knuth撰写的一篇论文[21]提倡将它用于算法分析。在算法性能界限的数学表述方面，这些符号已经被广泛使用。符号O表示上界；符号Ω表示下界；符号Θ表示同时有上界和下界。
在数学中，符号O最常见的用法是表示渐近近似的相关内容。我们将在第4章讨论这种用法。在算法理论中，符号O通常用于三种目的：一是隐藏可能无关紧要或计算不便的常量；二是在描述算法运行时间的表达式中表示相对较小的“错误”项；三是限制最坏情况。如今，符号Ω和符号Θ直接与算法理论相关，不过类似的符号在数学中也有使用（见参考资料[21]）。
由于忽略了常数因素，对使用这些符号的数学结果进行推导，比寻求更精确的答案要简单。例如，自然对数
和二进制对数
经常出现，且由一个常数因素相关联，所以如果不要求高精确度，可以把这两个对数都用O(logN)表示。更重要的是，如果只对基本操作执行频率进行分析，我们可以说，算法的运行时间是Θ(NlogN)秒；并且，如果不需要计算出常数的精确值，则可以假设在指定的计算机上，每个操作需要恒定的时间。
习题1.1 证明
与 
相等。
作为运用这些符号来研究算法性能特点的例证，我们考虑一下对数组中的数字进行排序。输入是数组中的数，这些数以任意未知的顺序排列；输出是该数组中相同的数，但按照升序排列。这是一个值得深入研究的基本问题：我们先来考虑解决这个问题的算法，然后在技术意义上，证明该算法是“最优”的。
首先，要证明著名的递归算法，即Mergesort，这样能够有效地解决排序问题。Mergesort和本书中几乎所有的算法都由Sedgewick和Wayne在参考资料[30]中进行了详细论述，所以在这里只给出简单的介绍。对各种算法、实现和应用的进一步细节有兴趣的读者，可以参考资料[6]、[11]、[17]、[18]、[19]、[20]、[26]以及其他资料。
Mergesort把数组从中间分开，对两部分（递归地）排序，然后把排好顺序的两部分合并在一起，得到排序的结果，如Java程序1.1实现的这一功能。Mergesort是著名的分治（divide-and- conquer）算法设计范例的典型代表，这类算法先（递归）解决难度较小的子问题，然后用子问题的结果来解决初始问题。我们将在本书中分析一些这样的算法，诸如Mergesort算法这样的递归结构，通过分析会很快得到其性能特点的数学表达。
为了完成合并，程序1.1使用了两个辅助数组b和c来保存子序列（为了提高效率，最好在递归方法之外声明这些数组）。通过mergesort(0,N-1)调用这一方法对数组a[0…N-1]进行排序。调用递归算法之后，数组的两部分完成排序。再把a[ ]的前半部分复制到辅助数组b[ ]，把a[ ]的后半部分复制到辅助数组c[ ]。我们增设一个“警戒标记”INFTY，它比每个辅助数组末尾的所有元素都大。当一个辅助数组已经没有元素时，“警戒标记”INFTY能够帮助另一个辅助数组将剩下的部分转移到数组a。在这些准备条件下很容易完成合并：k每取一次新的值，就把b[i]和c[j]中较小的那个元素移动到a[k]，然后相应地增加k、i或者j。
程序1.1 Mergesort
习题1.2 在某些条件下，定义“警戒标记”值可能不方便或不切实际。实现一个不用定义“警戒标记”值的Mergesort（见参考资料[26]中介绍的各种方法）。
习题1.3 实现一种Mergesort，将数组分成三个相等的部分，先对这三部分排序，然后进行三向合并。将这一Mergesort的运行时间与标准Mergesort进行比较。
在当前情况下，Mergesort是重要的方法，因为它能保证与任何排序算法一样有效率。为使这个结论更加精确，我们首先分析Mergesort运行时间的主导因素，即所用的比较次数。
定理1.1（Mergesort比较） 如果对包含N个元素的数组进行排序，则Mergesort需要使用NlgN+O(N)次比较。
证明：若CN为程序1.1排列N个元素所需的比较次数，那么排列前半部分元素的比较次数是
，合并的比较次数是N（当下标k每取一次新的数值都有一次比较）。换言之，Mergesort的比较次数可由下面的递归关系准确表示
（1）
为得到这个递归关系的解的性质，我们考虑当N是2的幂时的情况
将方程的两边除以2n，我们发现
这证明了，当
时，
；对于N的一般情况，定理可由式（1）归纳证明。实际上，准确结果是相当复杂的，它取决于N的二进制表示的性质。在第2章，我们将详细讨论如何求解这样的递归关系。
习题1.4 求能够表示
的递归关系，并利用这一关系证明
习题1.5 证明
。
习题1.6 分析习题1.2中提到的三向Mergesort所使用的比较次数。
对于大多数计算机而言，程序1.1所用的基本操作的相对开销与常数因子相关，因为这些操作均为一个基本指令周期的整数倍。此外，程序的整体运行时间在比较次数的常数倍范围内。因此，我们可以合理假设：Mergesort算法的运行时间在NlgN的常数倍范围内。
从理论上讲，Mergesort表明NlogN是排序问题固有性难点的“上界”。
存在一种算法，能够以与NlgN成正比的时间，将任意N-元素文件排序。
充分证明这一结论需要根据相关操作和所用的时间，谨慎构建所需的计算机模型，但其结果却是在相对宽松的假设下得出的。我们说，“排序的时间复杂度是O(NlogN)”。
习题1.7 假设Mergesort的运行时间是
，其中c和d是与机器相关的常数。证明：如果我们在特定的计算机上运行这个程序，并观察到对应某一值N的运行时间是tN，那么对于2N，我们可以精确估计运行时间是
，此结果与机器因素无关。
习题1.8 在一台或多台计算机上实现Mergesort，观察
时的运行时间，并根据前面的习题预测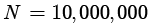
时的运行时间。然后观察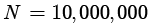时的运行时间，并计算预测的准确度百分比。
这里实现Mergesort的运行时间仅仅取决于用于排序的数组中的元素个数，而不是它们的排列方式。对于许多其他排序算法而言，其运行时间是输入序列初始顺序的函数，因此运行时间会因为初始顺序的不同而产生很大的变化。一般来讲，在算法理论中，我们更关注最坏情况的性能，因为这可以体现算法的性能特点，而不再受输入的影响；在特定算法的分析中，我们最关注平均情况的性能，因为它能够提供一种方法来预测“典型”输入的算法性能。
我们总是寻求更好的算法，那么自然而然会出现一个问题：是否存在一种排序算法，它比Mergesort具有更好的渐近性能？下面源于算法理论的经典结果说明，本质上不存在这样的算法。
定理1.2（排序复杂度） 对于某些输入，任何基于比较的排序至少要进行
次比较。
证明：这个结论的完整证明在参考资料[30]和[19]中。直观地看，每次比较最多能将所考虑元素的可能排列数量减少一半，根据这一事实我们可以推出结果。由于排序之前有N！种可能的排列方式，而目标是排序后仅得到其中一种排序，将N！一直除以2直至结果小于统一的数值，则比较的次数必定至少为进行除法计算的次数，即[lgN!]。根据Stirling的渐近阶乘函数能够得出该定理的结论（见定理4.3的第2个推论）。
从理论角度出发，结果表明NlogN是排序问题固有性难点的“下界”。
如果将一个N-元素的输入文件排序，那么所有基于比较的排序算法所需时间都与NlgN成正比。
这是关于一整类算法的一般说明。我们将其概括为“排序的时间复杂度是Ω(NlogN)”。这个下界很重要，因为它与定理1.1的上界相匹配，进而表明没有算法比Mergesort具有更好的渐近运行时间，在此意义上，Mergesort是最优的。我们将其概括为“排序的时间复杂度是Θ(NlogN)”。从理论角度出发，这完成了排序“问题”的“解”：已证明上界和下界是匹配的。
再次指出，这些结论在一般的假设下是成立的，尽管它们或许不像看起来那样普通。例如，结论没有提及不基于比较的排序算法。事实上，存在基于指数计算技术的排序算法（如第9章讨论的算法），这些算法以平均线性时间运行。
习题1.9 假设已知两个不同的值，N-元素数组任意元素的取值是这两个不同值之一。设计一个排序算法，使其所需时间与N成正比。
习题1.10 当从三个不同值中取值时，给出习题1.9的答案。
在定理1.1和定理1.2的证明中，我们忽略了许多关于计算机和程序正确建模的细节。算法理论的本质是构建完善的模型，可以据此评估重要问题的固有性难点，还可以研究“有效”算法，这些算法体现了匹配相应下界的上界。对于许多重要问题范畴，在渐近最坏情况性能方面，下界和上界之间仍然存在明显差距。算法理论为研究解决这类问题的新算法提供了指导。我们需要能够降低已知上界的算法，但是寻找比已知下界性能更好的算法往往难以实现（寻找那种破坏模型条件的算法或许可行，然而下界却建立在模型条件的基础之上）。
因此算法理论提供了一种方法，能够根据算法的渐近性能将算法分类。然而，（在一个常数内）近似分析的过程经常限制我们准确预测任何特定算法性能特点的能力，尽管近似分析的确拓展了理论结果的适用性。更重要的是，算法理论通常基于最坏情况分析，这样的结果可能过于悲观，而且在预测实际性能方面最劣情况分析不如平均情况分析那样实用。这对Mergesort之类的算法（其运行时间与输入关系不大）是无关紧要的，但正如我们所看到的那样，平均情况分析有助于我们认识到：有时非最优算法在实际操作中更快一些。算法原理可以帮助我们鉴别优秀的算法，但是为了更好地比较和改进算法，我们有必要完善分析。要做到这一点，我们需要关于所用特定计算机性能特点的准确知识，以及精准确定基本操作执行频率的数学技术。在本书中我们会研究这样的技术。
1.3 算法分析概述虽然在1.2节中我们对排序和Mergesort的分析证实了排序问题的固有性难点，但仍然尚未涉及与排序（和Mergesort）相关的许多重要问题。在特定计算机上运行Mergesort算法的实现方法，预计可能需要多长时间？如何将其运行时间与其他运行时间为O(NLogN)的算法（这样的算法有很多）相比较？某些排序算法在平均情况下运行速度很快，但在最劣情况下可能没那么快，如何将其与这样的算法做比较？如何将其与不基于元素间比较的排序算法做对比？要回答这样的问题，则需要更细致的分析。本节我们简要描述进行这样分析的过程。
为了分析算法，首先我们必须明确最具价值的重要资源，以便能够正确而集中地进行细致分析。我们从研究运行时间的角度来描述分析过程，因为运行时间在此处是与之最相关的资源。一个算法所需运行时间的完整分析包括以下步骤。
● 完整地实现算法。
● 确定每个基本操作所需的时间。
● 识别能够用于描述基本操作执行频率的未知量。
● 为程序的输入建立一个实际模型。
● 假设输入模型已经建立，分析其中的未知量。
● 将每个操作的频率乘以操作的时间，然后把所有的乘积相加，计算出总的运行时间。
分析的第一步是为了在特定计算机上严谨地实现算法。如果我们用术语程序（program）一词来描述这样的实现，那么可以说一种算法与多个程序相对应。一个特定的实现不仅能提供具体的研究对象，还能提供有用的经验数据以帮助或检验分析。算法的实现应该设计得能够有效利用资源，而在设计的过程中不应该过早过分地强调效率。事实上，分析主要是为更好地提供知识方面的指导。
下一步是估计构成程序的每个指令所需要的时间。在实际操作中，我们可以非常精确地完成这个过程，但这个过程很大程度上取决于所用机器的系统特性。另一种方法是对少量的输入直接运行程序来“估计”常量的值，或者像习题1.7描述的那样，总体上间接地进行。本书中我们没有详细研究这个过程，而是集中关注分析中“与机器无关”的部分。
事实上，为了确定程序的总体运行时间，必须研究程序的分支结构，以便用未知数学量表示程序构成指令的执行频率。如果这些量的值是已知的，那么我们可以直接将每个程序构成指令的所需时间乘以频率，然后把这些乘积相加，进而得到整个程序的运行时间。许多编程环境有简化这项工作的工具。在分析的第一阶段，我们关注具有大频率值或对应开销较高的量；原则上来讲，分析能通过精简得到足够详尽的答案。当环境允许时，我们经常把算法的“开销”作为“所讨论的量的值”的简称。
下一步是为程序的输入建模，也是为指令频率的数学分析打下基础。未知频率值取决于算法的输入：输入的大小（我们通常称之为N）往往是表示结果的重要参数，但输入数据的顺序或输入数据值通常也影响运行时间。这里的“模型”是指对算法典型输入的准确描述。例如，对排序算法来说，比较方便的做法通常是假设输入数据随机排序且互异，尽管当输入数据非互异时程序也能正常运行。排序算法的另一种可能是假设输入取自范围相对较大的随机数。我们能够证明这两种模型几乎是等价的。大多数情况下，我们使用最简单的“随机”输入模型，因为这种模型通常更切合实际。几种不同模型也可以用于同一算法：一种模型的选用可能使分析变得尽可能简单，而另一种模型可能会更好地反映即将运行的程序的实际情况。
最后一步是假设输入模型已经建立，要分析其中的未知量。对于平均情况分析，我们逐个分析这些量，然后用指令次数乘以相应的平均值，并把乘积相加，进而得到整个程序的运行时间。对于最坏情况分析，得到整个程序的准确结果往往是很困难的，所以我们只能通过将指令次数乘以每个量的最坏情况值，然后把结果相加得到上界。
在许多情况下，这种场景可以成功地提供准确的模型。Knuth的著作——参考资料[17]、[18]、[19]、[20]正是基于这一概念。不幸的是，如此精细的分析所涉及的细节常常令人望而生畏。因此，我们通常寻找能够使用的近似（approximate）模型来估计开销。
使用近似模型的第一个原因是：在现代计算机具有复杂体系结构和操作系统的条件下，确定所有独立操作的开销细节几乎是无法实现的。因此，我们通常在程序的“内部循环”中只研究很少的一些量，推测仅通过分析这些量就能准确地估计成本。有经验的程序员通过定期“验证”相关实现来确定“瓶颈”，这是确定此类量的系统方法。例如，我们往往仅通过记录比较次数来分析基于比较的排序算法，这种方法存在机器无关（machine independent）的严重副作用。通过仔细分析比较算法使用的比较次数，我们能够预测许多不同计算机的性能。相关假设很容易通过实验验证，从原则上来讲，我们可以在适当的情况下完善它们。例如，我们可以改进基于比较的排序模型，使之包含数据移动，而这可能又需要考虑缓存的影响。
习题1.11 在两台不同的计算机上运行实验来验证这样一个假设，即随着问题大小的增加，Mergesort的运行时间除以它使用的比较次数，其结果趋近于一个常数。
近似对数学模型同样有效。使用近似模型的第二个原因是：避免我们推导的用于描述算法性能的数学公式中存在不必要的复杂性。以此为目的研究经典近似方法是本书的重要内容，我们将提供很多例子。除此之外，现代研究对算法分析的一个主要推动来自研究基础数学分析的方法。准确地说，这些方法可以用于准确地预测性能和比较算法，而且从原则上来讲，我们还可以对其进行改进以达到手头应用所需要的精度。这些技术主要涉及复杂的分析，参考资料[10]中充分介绍了相关内容。
1.4 平均情况分析在本书中，我们讨论的数学技术不仅适用于解决与算法性能相关的问题，还适用于构建从基因组学到统计物理学等各种科学应用的数学模型。因此，我们经常考虑广泛适用的结构和技术。然而，我们的主要目的是研究所需要的数学工具，以便能够在实际应用中对重要算法的资源使用做出准确的说明。
我们专注于分析算法的平均情况（average-case）：我们设计一个合理的输入模型，分析一个程序的预期运行时间，程序的输入从这个模型中提取。该方法之所以有效，是因为以下两个主要原因。
平均情况分析在现代应用中重要而有效的第一个原因是，随机性的简单模型通常是非常准确的。以下是排序应用的几个代表性示例。
● 排序是密码分析（cryptanalysis）的一个基本过程，密文已经在很大程度上使数据与随机数据不可区分。
● 商业数据处理（commercial data processing）系统通常需要排序巨大的文件，其中密钥往往是账号或其他标识号，这些号码利用适当范围内的均匀随机数进行良好建模。
● 计算机网络（computer networks）的实现依赖于再次涉及被随机数模型化的密钥的种类。
● 排序广泛应用于计算生物学（computational biology），其中与随机性的显著偏差由科学家进一步研究，以试图了解基本的生物和物理过程。
如这些示例所示，简单的随机模型很有效，不仅能用于分类应用，也可在实践中广泛用于各种基础算法。一般来说，当人们创建大型数据集时，这些数据集通常是基于随机模型任意构建的。随机模型在处理科学数据方面经常也是有效的。爱因斯坦曾反复劝告我们——在这种情况下“上帝不玩色子”，意思是：随机模型是有效的，因为如果发现与随机性相比有明显偏差，我们就已经学到了一些有关自然界的重要东西。
平均情况分析在现代应用中重要而有效的第二个原因是，我们经常可以将随机性赋予一个问题实例，使其对于算法（和分析者）来说，看起来是随机的。这是设计具有可预测性算法的有效方法，也称其为随机算法（randomized algorithms）。M.O. Rabin [25]是该算法的最初提出者之一，此后，许多其他研究人员发展了该算法。Motwani和Raghavan的著作[23]深入介绍了这一内容。
因此，我们首先分析随机模型，这通常从计算平均值开始——随机抽取N个实例，计算其有价值的量的平均值。现在，t（尽管密切相关）的方法来计算某个量的平均值。在本书中，我们将明确讲解以下两种计算平均值的不同方法。
令
是大小为N的可能的输入数据的数量，令
是使算法开销为k且大小为N的输入数据的数量，所以
。此时，开销为k的概率是
，开销的数学期望是
算法的分析依赖于“计数”。大小为N的输入数据有多少个？使算法开销为k且大小为N的输入数据有多少个？这些是计算开销为k的概率的步骤，所以这种方法可能是初等概率论中最直接的方法。
令
是算法对所有大小为N的输入的总（或累积的）开销。（即
，只是通常不必用这种方法计算。）此时平均开销是
。算法的分析取决于不太具体的计数问题：在所有输入的基础上，算法的总开销是多少？我们将使用一般工具，让这种方法变得非常有吸引力。
分配方法提供了完整的信息，可以直接用于计算标准差和概率论中其他的矩。正如我们将要看到的那样，在使用累积法时，间接方法（常常更简单）也能用来计算这些矩。在本书中，尽管我们更倾向于采用累积法，而且这也最终促使我们用基本数据结构的组合属性来研究算法分析，但我们还是对两种方法都做了研究。
许多算法是通过递归地求解较小的子问题来解决问题的，因此这些算法服从平均开销或总开销必须满足的递归关系的推导。正如下一节的示例所示，从算法直接推导出递归关系常常是一种自然的处理方式。
无论平均情况的结果是如何得到的，我们都更关注这个结果，因为在随机输入是合理模型的大多数情况下，准确的分析可以帮助我们：
● 针对同一任务比较不同算法；
● 预测具体应用所需的时间和空间；
● 比较将要运行同一算法的不同计算机；
● 调整算法参数以优化性能。
把平均情况的结果与经验数据进行比较，以检验算法的实现、模型和分析。在特定应用中，不论将其置于何种环境下，用平均情况的结果都可以预测算法如何表现，最终正是为了对此获得足够的信心。如果希望评估新机器架构对重要算法性能的影响，也许我们可以在新的架构出现之前通过分析来实现。这种方法的成功在过去几十年中得到了验证：50年前我们第一次分析了本节涉及的排序算法，其分析结果仍然有助于评估这些算法在如今的计算机上的表现。
1.5 实例：快速排序算法的分析为了说明被忽略的基本算法，我们研究下一个相当重要的特殊算法——快速排序算法。该算法是在1962年由C.A.R. Hoare提出的，他的论文[15]是算法分析中较早而且十分出色的典范。Sedgewick[27]（也可见参考资料[29]）也将快速排序算法的分析论述得很详细，我们在此仅针对其重点进行阐释。详细研究这种分析是值得的，不仅是因为该排序方法使用广泛，其分析结果直接与实践相关，也是因为分析本身就能说明许多问题，这些问题我们将会在本书的后面遇到。特别的是，相同的分析也适用于树结构基本性质的研究，这种结构具有广泛的价值和适用性。更一般地说，对快速排序算法的分析表明了我们如何分析一种广泛的递归程序。
程序1.2是快速排序算法在Java中的实现。这是一个递归程序，通过将数组分成两个独立（较小）的部分，然后将这两部分分别排序，从而实现对整个数组的排序。显然，当遇到空的子序列时，递归终止，而我们设计的算法实现也会将大小是1的子序列作为停止点。
程序1.2 快速排序算法
这个细节似乎无关紧要，但正如我们将看到的那样，递归的本质就是确保程序将被用于大量的小分支，而这种简单的改进可以显著提升性能。
划分过程把位于数组最后位置上的元素（分隔元，partitioning element）放入正确的位置，使其之前的元素都比它小，之后的元素都比它大。该程序使用两个指针来实现划分：一个指针从左边扫描数组，另一个指针从右边扫描数组。左指针递增，直至找到大于分隔元的元素；右指针递减，直至找到小于分隔元的元素。然后把两个元素交换，并且该过程继续，直至指针相交，此时的位置就是分隔元的放置位置。确定位置后，程序用a[hi]替换a[i]，把分隔元放入指定位置。最后调用quicksort(a,0,N-1)完成数组排序。
有几种方法能实现刚刚概述的一般递归策略；上面描述的实现方法取自参考资料[30]（也可见参考资料[27]）。以分析为目的，我们假设数组a包含随机排序的不同数值，但请注意，此代码对于所有输入（包括相等的数字）都能正常工作。也可以在更切合实际的模型下研究这个程序，即允许相等的数值（见参考资料[28]）、长字符串关键字（见参考资料[4]）以及许多其他情况。
一旦实现了算法，分析的第一步就是估计这个程序各个指令的资源需求。这取决于特定计算机的性能，所以我们忽略这些细节。例如，“内层循环”指令：
在一般计算机上可能会将其转换为汇编语言指令，如下所示。
该循环的每次迭代可能需要4个单位时间（每个内存引用一个）。在现代计算机上，由于缓存、管道以及其他影响，准确地估计开销变得更为复杂。内循环中的另一个指令（递减j）与上面的指令（递加i）是相似的，但是需要额外检验判断j是否超出边界。但如果使用警戒标记，就无须进行额外检验，所以我们可以忽略其多余的复杂性。
分析的下一步是将变量名分配给程序中指令的执行频率。正常情况下只涉及少数真变量：所有指令的执行频率都可以用这些变量表示。此外，我们希望将这些变量与算法本身相关联，而不是任何特定程序。快速排序算法涉及3个自然量：
A——分隔阶段数；
B——交换次数；
C——比较次数。
在一般计算机上，快速排序算法的总运行时间可以用公式表示，即
（2）
这些系数的精确值取决于编译器生成的机器语言程序和所使用的计算机的属性；上面给出的是典型值。比较在同一计算机中实现的不同算法时，这个表达式是很有用的。事实上，即使Mergesort是“最优”算法，Quicksort仍具有重要的实际意义，其原因在于：Quicksort每次比较的开销（C的有效性）可能明显低于Mergesort的开销，进而导致在一般实际应用中Quicksort的运行时间明显缩短。
定理1.3（Quicksort分析） 对N个顺序随机且元素互异的数组排序，Quicksort平均使用
个分隔阶段，
次比较，
次交换。
证明：在这里，准确的答案用调和级数
表示，这是我们在算法分析中将会遇到的许多著名“特殊”数列中的第一个。
与Mergesort一样，Quicksort的分析涉及定义和求解直接反映算法递归性质的递归关系。但在这种情况下，递归必须基于关于输入的概率表述。如果CN是排列N个元素的平均比较次数，则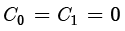
且
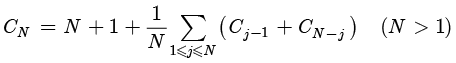（3）
为了得到总的平均比较次数，我们把第一次分隔阶段的比较次数（
）加到用于分隔后的子序列的比较次数中。当分隔元是第j个最大元素（对于每个
，其出现的概率是1/N）时，分隔后的子序列大小分别为
和 
。
现在，分析被简化为数学问题式（3），它已经不依赖于程序或算法的性质了。这种递归关系比公式（1）稍微复杂一些，因为公式的右边直接取决于前面所有的值，而且这些值不止几个。尽管如此，求解式（3）也并不困难：首先在和的第二部分中把j变为
，得到
然后乘以N，减去当数组元素个数为
时的同一个公式，消除求和项后得到
再重新排列各项，得到一个简单的递归
两边同时除以
，得
重复代入，最后剩下
这就完成了证明，因为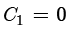
。
如上所述，每个元素都用于一次分隔，因此阶段总数为N；先计算第一次分隔阶段的平均交换次数，就可以从这些结果中得到平均交换次数。
该定理所述的近似值由著名的调和级数近似值
得到。我们将在第4章仔细研究这种近似。
习题1.12 给出Quicksort对N个元素的N！种全部排列所用比较总次数的递归。
习题 1.13 证明分隔随机排列之后得到的子序列本身都是随机排列。然后证明，如果分隔时右指针初始化为j:=r+1，那么情况会有所不同。
习题1.14 按照上面的步骤求解递归
习题1.15 证明第一次分隔阶段（在指针交叉之前）用的平均交换次数是(N-2)/6。（因此，根据递归的线性性质，
。）
通过生成随机输入数据到程序并计算所用比较次数可得到经验数据，图1.1显示了分析结果与这些经验数据的比较。每次实验用灰色点描述经验结果（图中显示的每个N值对应100次实验），黑色点表示N的平均值。分析结果是一条平滑曲线，它拟合了定理1.3给出的公式。正如预期的那样，曲线拟合得非常好。
图1.1 Quicksort所需比较次数：经验结果和分析结果
例如，定理1.3和公式（2）说明，在前面描述的特定机器上，对一个N元素的随机序列进行排序，Quicksort大约需要11.667NlnN-0.601N个步骤；而对于其他机器，也可以像公式（2）和定理1.3讨论的那样，通过考查机器的性质推导出类似的公式。这种公式可用于（非常准确地）预测Quicksort在特定机器上的运行时间。更重要的是，它们可用于估计和比较算法的变量，并为其效果提供量化证据。
因为适当关注细节能够排除机器依赖性，所以本书中我们通常专注于分析与一般算法相关的量，例如“比较”和“交换”。这不仅使我们集中精力于分析的主要技巧，还可以扩展结果的适用性。例如，排序问题的一个较广泛的特点是：将待排序元素视为除排序关键字（key）之外的其他信息的记录（record）。因此访问一个记录（取决于记录的大小）可能比进行一次比较（取决于记录和关键字的相对大小）的开销更昂贵。然后，我们从定理1.3得知，Quicksort比较关键字约2NlnN次，移动记录约0.0667NlnN次，并且我们能更加精确地估计开销或在适当的时候与其他算法进行比较。
Quicksort可以通过多种方式改进自身，成为在许多计算环境下被优先选择的排序方法。我们甚至可以分析复杂的改进版本，并得出平均运行时间的表达式[29]，而且该表达式紧密地匹配所观察到的经验数据。当然，提出的改进方法越复杂，分析也就越复杂。可以通过扩展以上给出的论证来处理某些改进，但是另一些改进则需要更强有力的分析工具。
Quicksort最简单的变体是基于下面的观察结果：对于非常小的序列，Quicksort不是非常有效（例如，如果对大小为2的序列进行排序，只需一次比较，可能还要一次交换），所以比较小的序列应该用更简单的排序方法。下面的习题说明了如何通过扩展以上分析结果来研究一种混合算法，其中“插入排序”（见7.6节）用于长度小于M的序列。那么，这种分析方法有助于选择参数M的最优值。
习题1.16 当用Quicksort对一个大小为N的随机序列进行排序时，平均能遇到多少长度小于或等于2的子序列？
习题1.17 如果我们把前面实现快速排序算法程序的第一行改为
那么排序N个元素所需的总比较次数可由下面的递归关系描述
根据定理1.3中的证明方法准确解出该递归关系。
习题1.18 忽略习题1.17的答案中的较小项（明显小于N的项），求函数f(M)，使比较次数近似于
画出函数f(M)，并找出将该函数最小化的M值。
习题1.19 当M变大时，比较次数从刚刚推导的最小值增加。M增加到多大时，才能使比较次数超过原来（当M=0时）的次数？
Quicksort的自然改进就是使用如下抽样：选取小样本，然后将样本的中值作为分隔元，这样估计的分隔元更可能接近于序列的中值。例如，如果我们把3个元素作为一个样本，那么这种“三数中值”Quicksort所需的平均比较次数可由下面的递归关系描述
（4）
其中
是二项式系数，表示从N项中选取3项的选取方法的数量。因为第k个最小元素是分隔元的概率为
（与正常Quicksort的1/N相反），所以上面的公式成立。我们希望能够求解这种性质的递归关系，以便确定需要使用多大的样本以及何时切换到插入排序。然而，求解这种递归关系需要使用的技巧比迄今为止所涉及的技巧都要复杂。在第2章和第3章，我们将学习准确求解这种递归的方法，这些方法能够确定参数的最佳值，例如样本大小和小型子序列的分割。根据这些方面的广泛研究得出结论：对于一般实现方法而言，三数中值Quicksort运用从10到20范围内的截止点，使实现接近最佳性能。
Quicksort的另一种变体利用了下面这一事实：关键字可以被视为二进制字符串。我们分隔序列不是通过比较序列中的关键字，而是通过把所有前导位是0的关键字都置于所有前导位是1的关键字之前。然后，将得到的子序列用第二位以相同的方式进行独立地分隔，以此类推。Quicksort的这种变体叫作“基数—交换排序”或“基数Quicksort排序”。那么这种变体与基本算法如何比较呢？为了回答这个问题，首先我们必须注意：因为由随机位组成的关键字与随机排列有本质上的区别，所以需要用到不同的数学模型。“随机位串”模型可能更加切合实际，因为它反映了实际的表示法，但可以证明这两个模型大致上是等价的。在第8章我们将更加详细地讨论这个问题。通过类似上面给出的证明方法，可以证明：这种方法所需的位平均比较次数可由下面的递归关系描述
事实证明，这个递归关系比前面给出的递归关系更难求解——在第3章，我们将看到母函数把这个递归关系转换为CN的明确数学公式；在第4章和第8章，我们将学习如何得到一个近似解。
这种分析方法在适用性上有局限性——上述所有递归关系均取决于算法的“保持随机性”性质：如果原序列是随机排序的，那么可以证明，分隔后的子序列也是随机排序的。算法的实现没有这样的限制，而且算法广泛使用的许多变体也不符合该性质。这种变体似乎非常不利于分析。幸运的是（从分析学家的角度来看），经验研究表明，这种变体的性能也同样不佳。因此，虽然没有进行分析量化，但保持随机性的要求似乎有助于设计出更精致、更有效的Quicksort实现方法。更重要的是，如前所述，保持随机性的算法确实得到了性能上的改进，而且这些改进完全可以从数学上量化。
数学分析在Quicksort实际变体的研究中发挥着重要作用。而且我们将看到，还有许多其他问题需要考虑，其中详细的数学分析是算法设计过程的重要组成部分。
1.6 渐近近似在前面给出的关于Quicksort平均运行时间的结论中得到的是准确结果，但我们还给出了一个以著名函数表示的更简捷的近似表达式，这些著名的函数用来计算准确的数值估计。正如我们将看到的那样，通常来讲，准确结果是很难得到的，或者说得出和解释近似结果至少要容易得多。理想情况下，我们分析算法的目的是得出准确结果；但从实用角度来看，能够做出有用的性能预测，力求导出简捷而准确的近似答案，可能更符合我们的总体目标。
为此，我们需要处理这些近似值的经典技巧。在第4章，我们将研究Euler-Maclaurin求和公式，它提供了一种用积分估计求和的方法。因此，我们可以通过计算
得到近似调和级数。然而，≈的意义还可以更精确，例如，我们可以断定
，其中
是一个常数，在分析中叫作欧拉常数（Euler constant）。虽然没有规定符号O中隐含的常数，但这个公式提供了一种估计HN值的方法，即随着N的增加，估计的HN精度越来越高。此外，如果我们想要估计得更加精确，那么可以推导出一个HN精确到O(N-3)甚至
的公式，其中k为任意常数。这种近似方法称为渐近展开（asymptotic expansions），是算法分析的核心，也是第4章的主要内容。
渐近展开的使用可以看作在精确结果（这是理想的目标）与简捷近似（这是实际的需求）之间的一种折中。事实证明，一方面，如果需要，我们通常有能力得出更准确的表达式，但另一方面，我们又没有这样的需求，因为仅含有几项的展开式（如上面HN的表达式）就能将答案精确到多位小数。我们一般用符号≈对结果求和，而不是命名无理常数，例如，定理1.3的结论就是如此。
此外，准确的结果和渐近近似都受制于概率模型所固有的不准确性（这种模型通常都是现实的理想化）和随机波动。表1.1显示了对于不同大小的随机序列，Quicksort所用比较次数的准确值、近似值和经验值。准确值和近似值由定理1.3给出的公式计算得出；经验值是选取100个序列，然后测出的平均值，这些序列由小于106的随机正整数构成。这不仅检验我们讨论的渐近近似，还检验我们所使用的随机排序模型固有的“近似”（忽略了相等关键字）。出现相等关键字时的Quicksort分析在参考资料[28]中有介绍。
表1.1 Quicksort使用的平均比较次数
| 序列大小 |
准确值 |
近似值 |
经验值 |
|---|---|---|---|
| 10,000 |
175,771 |
175,746 |
176,354 |
| 20,000 |
379,250 |
379,219 |
374,746 |
| 30,000 |
593,188 |
593,157 |
583,473 |
| 40,000 |
813,921 |
813,890 |
794,560 |
| 50,000 |
1,039,713 |
1,039,677 |
1,010,657 |
| 60,000 |
1,269,564 |
1,269,492 |
1,231,246 |
| 70,000 |
1,502,729 |
1,502,655 |
1,451,576 |
| 80,000 |
1,738,777 |
1,738,685 |
1,672,616 |
| 90,000 |
1,977,300 |
1,977,221 |
1,901,726 |
| 100,000 |
2,218,033 |
2,217,985 |
2,126,160 |
习题1.20 在由104个小于106的随机整数构成的序列中，有多少关键字可能等于该序列中的其他关键字？运行仿真或进行数学分析（借助于数学计算系统），或两者都做。
习题1.21 用由小于M的随机正整数组成的序列进行实验，其中M=10,000、1000、100或其他值。比较Quicksort作用于这种序列的性能与其作用于相同大小的随机序列的性能。描述使随机排序模型不准确的情况的特征。
习题1.22 如何用类似于表1.1的表格来描述Mergesort的相关特点，讨论这个想法。
在算法理论中，符号O用于隐去所有细节：语句“Mergesort需要O(NlogN)次比较”隐藏了除算法、实现和计算机最基本特征之外的所有内容。在算法分析中，渐近展开提供了一种可控的方式来隐藏不相关的细节，与此同时保留了最重要的信息，尤其是涉及常数因子的信息。功能强大的一般分析工具直接进行渐近展开，因此常常可提供简捷而准确地描述算法性质的表达式的简单直接结论。有时我们利用渐近（估计）来提供比其他方式更准确的程序性能描述。
1.7 分布一般来说，概率论告诉我们：关于开销分布
的其他事实也与我们对算法性能特点的理解有关。幸运的是，对于我们在算法分析中研究的几乎所有例子，实际上只要知道平均值的渐近估计就足以做出可靠的预测。我们在这里回顾几个基本概念。对概率论不熟悉的读者可以参考任何一本标准教材——例如参考资料[6]。
当N取较小值时，Quicksort所用比较次数的完整分布如图1.2所示。对于N的每个取值，画出点CNk/N!，这是使Quicksort需要进行k次比较的输入比例。因为每条曲线都是完整的概率分布，所以曲线下方的面积为1。平均值2NlnN+O(N)随着N的增加而增加，因此曲线向右移动。针对相同数据略微不同的观察结果如图1.3所示，其中每条曲线的水平轴适当缩放以便将平均值近似地置于中心，并稍微平移以分离这些曲线。这表明，该分布收敛于“极限分布”。
图1.2 Quicksort中比较次数的分布
本书中研究的大多数问题中，不仅确实存在这样的极限分布，而且我们还能精确地描述它们的特征。对于包括Quicksort在内的许多其他问题来说，这是一个重要挑战。然而很明显，这种分布集中在平均值附近（concentrated near the mean）。这种情况是常见的，事实上我们能够对这种结果做精确的表述，并且无须学习关于该分布的更多细节。
图1.3 Quicksort中比较次数的分布（缩放并平移到中心且分离曲线）
正如前面讨论的那样，如果是大小为N的输入组数，是大小为N且使算法开销为k的输入组数，那么平均开销可表示为
方差（variance）被定义为
标准差（standard deviation）是方差的平方根。知道平均值和标准差通常就能可靠地预测性能。完成这项工作的经典分析工具是切比雪夫不等式（Chebyshev inequality）：某一次观察值大于标准差与平均值之间距离的c倍的概率小于1/c2。如果标准差明显小于平均值，那么，随着N的增大，观察值很可能非常接近于平均值。这是算法分析中的常见情况。
习题1.23 本章前面给出的Mergesort实现所需比较次数的标准差是多少？
Quicksort所需平均比较次数的标准差是
（见3.9节），因此，参考表1.1，把
带入切比雪夫不等式，我们得出结论：存在超过90%的可能，当
时比较次数在2,218,033的205,004（9.2%）之内。这样的精度对预测性能来说肯定是足够的。
随着N的增加，相对精度也在增加。例如，当N增加时，分布变得更集中于图1.4所示的峰值附近。该图描绘了一个直方图，显示出Quicksort作用于10,000个不同随机序列所需的比较次数，其中每个序列都有1,000个元素。阴影区域表示超过94%的实验位于本次实验平均值的一个标准差之内。
图1.4 Quicksort比较次数的经验直方图（当
1,000时的10,000次实验）
对于总体运行时间，我们可以通过对每个量的平均值求和（乘以开销）得出，但计算总体运行时间的方差是一个复杂的计算过程。然而我们不必担心这一问题，因为总体方差与最大方差近似相等。当N取值很大时，与平均值相比，标准差相对较小，这解释了表1.1和图1.1观察的精度。在算法分析中总是发生这样的情况，如果我们对平均开销有一个精确的渐近估计，并且知道标准差渐近得更小，那么我们通常认为该算法已经“被完全分析”。
1.8 随机算法Quicksort平均情况性能的分析取决于随机顺序的输入。在许多实际情况下，这个假设可能不是严格有效的。一般来说，这种情况反映了算法分析中最严峻的挑战之一：需要适当地将可能在实际中出现的输入模型公式化。
幸运的是，常常存在能够规避这种缺陷的方法：在使用算法之前，先将输入“随机化”。对于排序算法而言，这相当于在排序之前将输入的序列随机排序。（相关算法的具体实现，请见第7章。）如果做到了这一点，那么前面提到的关于性能的概率论述就是完全有效的，并且无论实际中输入序列的顺序如何，都能准确地预测性能。
通过随机选择（与任意的特定选择相反），只要算法可以采用几种方案之一，就常常能够以较少的工作实现相同的结果。对于Quicksort，这个原理相当于随机选取元素作为分隔元，而不是每次都使用数组末尾的元素。如果这种方法能严谨地实现（保留子序列的随机性），则验证了先前的概率分析是有效的。（对于小型子序列应该使用截止的做法，因为它使生成随机数的数目大约减少 M。）随机算法的许多其他例子可以在参考资料[23]和[25]中找到。这种算法在实践中极具价值，因为它们利用随机性获得效率提升，并以高概率避免出现最劣情况的性能。此外，我们还可以对性能做准确的概率表述，进一步激励人们研究先进技术来获得这样的结果。
我们一直在考虑的关于Quicksort分析的例子可能说明了一种理想方法，但并不是所有的算法都能像这种方法一样被顺利地处理。像这样全面地进行分析需要花费相当多的精力，而这种精力应该留给最重要的算法。幸运的是，我们将看到存在许多基本方法，确实具备使分析值得深入进行的基本要素。
● 可以指定现实的输入模型。
● 可以推导出描述成本的数学模型。
● 可以得到简捷、准确的结果。
● 可以用结果来比较变体，可以与其他算法进行比较，而且有助于调整算法的参数值。
在本书中，我们考虑了许多这类方法，并重点研究使第2点和第3点成立的数学方法。
大多数情况下，我们跳过上述方法中程序特定（依赖于实现）的部分，是为了专注于算法设计，此时运行时间的粗略估计可能已经足够了；或者是为了专注于数学分析，此时数学问题所涉及的公式与求解方法是我们最感兴趣的问题。这些是涉及最重要的智力性挑战的领域，我们应该给予足够关注。
上文已经提到，目前在计算机的一般使用中，算法分析面临一个重要挑战，即如何把实际代表输入的模型以及易于进行分析问题的模型公式化。对此我们不必介意，因为存在一大类组合学（combinatorial）算法，对这类算法而言模型是自然的。在本书中，我们从一些细节入手考虑了这类算法的例子以及它们操作的基本结构。我们研究排列、树、字符串、字典树、单词和映射，是因为它们既是广泛研究的组合学结构，也是广泛使用的数据结构，还因为“随机”结构同时具备直接和现实的特点。
从第2章到第5章，我们着重讨论适用于算法性能研究的数学分析技术。除了算法分析，这些技术在许多其他应用中也非常重要。为了给本书后面的应用做准备，我们讨论的范围将进一步展开。然后，在第6章到第9章，我们将这些技术应用于分析某些基本的组合学算法，其中包含若干具有实际意义的问题。在各种各样的计算机应用中，这类算法中的许多算法都具有基础性的重要作用，因此需要对其进行详细分析。在某些情况下，有些看似很简单的算法却可能导致非常复杂的数学分析；而在另一些情况下，有些看上去相当复杂的算法却可能被直接简单地进行处理。在以上两种情况中，分析都能揭示在实际使用中具有直接影响的算法之间的重要区别。
重要的是，尽管现代计算机代数系统（例如Maple、Mathematica和Sage）在检查和开发结果方面是不可或缺的，但我们依旧要讲授并展现经典风格的数学推导。我们在这里提供的材料可以被视为学习如何有效利用这种系统的准备。
我们的重点是研究确定算法实现性能特征的有效方法。因此，我们所提供的程序都是以广泛使用的编程语言（Java）来编写的。这种方法具有一个优点，即程序是对算法完整而明确的描述。这种方法还有另一个优点，即读者可以通过运行经验测试来验证数学结果。我们的程序一般来源于Sedgewick和Wayne的Algorithms，4th edition[30]一书中的完整Java实现程序。我们尽可能地使用标准语言机制，以便熟悉其他编程环境的人能将其翻译为合适的编程语言。有关大多数程序的更多信息可以在参考资料[30]中找到。
当然，与介绍性材料中所讨论的内容相比，我们涉及的基本方法适用于更广泛的算法和结构。自20世纪中期计算机出现以来，研究者开发了大量组合算法，而我们仅讨论其中的几种。我们不涉及从图像处理到生物信息学等诸多应用领域，在这些领域中已经证明算法是有效的，并且已深入研究了某些算法。我们仅提及简单的方法，如平摊分析和概率性方法，这些方法已经成功应用于一些重要算法的分析。不过，为了鉴赏算法分析研究资料中的材料，我们希望读者通过掌握这本书的介绍性材料来做充足的准备。除了先前引用的Knuth、Sedgewick和Wayne以及Cormen、Leiserson、Rivest和Stein的图书，关于算法分析和算法理论的其他信息来源是参考资料[11]、参考资料[7]，以及参考资料[16]。
同样重要的是，我们讨论组合性的分析问题，它使我们能够开发一般的方法，这些方法可能有助于分析那些未来的、尚未被发现的算法。我们使用的方法源于组合学和渐近分析的经典领域，可以用这些领域中的经典方法来统一处理各种各样的问题。在我们的另一部书——Analytic Combinatorics[10]（《分析组合学》）中，对这一过程有详细的论述。最后，我们不仅能依据简单的形式描述直接将组合计数问题公式化，还可以直接根据这些公式推导出结果的渐近估计。
本书涵盖了重要的基本概念，而与此同时，参考资料[10]以及其他研究先进方法的书籍又为更先进的算法奠定了基础，例如Szpankowski有关字（有时也称为“单词”）的算法研究[32]，或者Drmota对树的研究[8]。参考资料[12]是涉及更多所用数学资料的良好来源；参考资料[5]（组合学）和参考资料[14]（用于分析）中也有相关内容。一般来说，我们在本书中运用初等组合学和实际分析，而参考资料[10]则从组合学角度来研究更先进的方法，它依赖于对渐近性的复杂分析。
经典数学函数的性质是本书内容的重要组成部分。由Abramowitz和Stegun撰写的Handbook of Mathematical Functions[1]（《数学函数手册》）内容经典，是数学家几十年来不可或缺的参考依据，当然也是本书创作的滥觞。最近出版了一个旨在取代它的新参考资料，并附有相关的在线资料[24]。实际上，在网络上，如维基百科（Wikipedia）和数学世界（Mathworld[35]）等资源中，能够越来越多地找到这种参考资料。另一个重要资源是Sloane的整数序列线上百科全书（On-Line Encyclopedia of Integer Sequences[31]）。
我们的出发点是研究那些广泛使用的基本算法的特点，但本书的主要目的是为我们遇到的组合学和分析方法提供连贯的处理。在适当的时候，我们详细研究那些自然产生但可能不适用于任何（当前已知）算法的数学问题。在使用这种方法的过程中，我们显然涉及范围和多样性的问题。此外，从全书的例子中可以看出，我们求解的问题与许多重要的应用直接相关。
参考资料[1] M. Abramowitz and I. Stegun. Handbook of Mathematical Functions, Dover, New York, 1972.
[2] A. Aho, J. E. Hopcroft, and J. D. Ullman. The Design and Analysis of Algorithms, Addison-Wesley, Reading, MA, 1975.
[3] B. Char, K. Geddes, G. Gonnet, B. Leong, M. Monagan, and S. Watt. Maple V Library Reference Manual, Springer-Verlag, New York, 1991. Also Maple User Manual, Maplesoft, Waterloo, Ontario, 2012.
[4] J. Clément, J. A. Fill, P. Flajolet, and B. Valée.“The number of symbol comparisons in quicksort and quickselect,” 36th International colloquium on Automata, Languages, and Programming, 2009, 750-763.
[5] L. Comtet. Advanced Combinatorics, Reidel, Dordrecht, 1974.
[6] T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein. Introduction to Algorithms, 3rd edition, MIT Press, New York, 2009.
[7] S. Dasgupta, C. Papadimititriou, and U. Vazrani. Algorithms, McGraw-Hill, New York, 2008.
[8] M. Drmota. Random Trees: An Interplay Between Combinatorics and Probability, Springer Wien, New York, 2009.
[9] W. Feller. An Introduction to Probability Theory and Its Applications, John Wiley & Sons, New York, 1957.
[10] P. Flajolet and R. Sedgewick. Analytic Combinatorics, Cambridge University Press, 2009.
[11] G. H. Gonnet and R. Baeza-Yates. Handbook of Algorithms and Data Structures in Pascal and C, 2nd edition, Addison-Wesley, Reading, MA, 1991.
[12] R. L. Graham, D. E. Knuth, and O. Patashnik. Concrete Mathematics, 1st edition, Addison-Wesley, Reading, MA, 1989.2nd edition, 1994.
[13] D. H. Greene and D. E. Knuth. Mathematics for the Analysis of Algorithms, 3rd edition, Birkh
user, Boston, 1991.
[14] P. Henrici. Applied and Computational Complex Analysis, 3 volumes, John Wiley & Sons, New York, 1974(volume 1), 1977(volume 2), 1986(volume 3).
[15] C. A. R. Hoare.“Quicksort,”Computer Journal 5, 1962, 10-15.
[16] J. Kleinberg and E. Tardos. Algorithm Design, Addison-Wesley, Boston, 2005.
[17] D. E. Knuth. The Art of Computer Programming. Volume 1:Fundamental Algorithms, 1st edition, Addison- Wesley, Reading, MA, 1968.3rd edition, 1997.
[18] D. E. Knuth. The Art of Computer Programming. Volume 2:Seminumerical Algorithms, 1st edition, Addison- Wesley, Reading, MA, 1969.3rd edition, 1997.
[19] D. E. Knuth. The Art of Computer Programming. Volume 3:Sorting and Searching, 1st edition, Addison- Wesley, Reading, MA, 1973.2nd edition, 1998.
[20] D. E. Knuth. The Art of Computer Programming. Volume 4A:Combinatorial Algorithms, Part 1, Addison- Wesley, Boston, 2011.
[21] D. E. Knuth.“Big omicron and big omega and big theta,”SIGACT News, April-June 1976, 18-24.
[22] D. E. Knuth.“Mathematical analysis of algorithms,”Information Processing 71, Proceedings of the IFIP Congress, Ljubljana, 1971, 19-27.
[23] R. Motwani and P. Raghavan. Randomized Algorithms, Cambridge University Press, 1995.
[24] F. W. J. Olver, D. W. Lozier, R. F. Boisvert, and C. W. Clark, ed., NIST Handbook of Mathematical Functions, Cambridge University Press, 2010. Also accessible as Digital Library of Mathematical Functions http:// dlmf.nist.gov.
[25] M. O. Rabin.“Probabilistic algorithms,”in Algorithms and Complexity, J.F.Traub, ed., Academic Press, New York, 1976, 21-39.
[26] R. Sedgewick. Algorithms (3rd edition) in Java: Parts 1-4:Fundamentals, Data Structures, Sorting, and Searching, Addison-Wesley, Boston, 2003.
[27] R. Sedgewick. Quicksort, Garland Publishing, New York, 1980.
[28] R. Sedgewick.“Quicksort with equal keys,”SIAM Journal on Computing 6, 1977, 240-267.
[29] R. Sedgewick.“Implementing quicksort programs,”Communications of the ACM 21, 1978, 847-856.
[30] R. Sedgewick and K. Wayne. Algorithms, 4th edition, Addison-Wesley, Boston, 2011.
[31] N. Slonae and S. Plouffe. The Encyclopedia of Integer Sequences, Academic Press, San Diego, 1995.Also accessible as On-Line Encyclopedia of Integer Sequences, http://oeis.org.
[32] W. Szpankowski. Average-Case Analysis of Algorithms on Sequences, John Wiley & Sons, New York, 2001.
[33] E. Tufte. The Visual Display of Quantitative Information, Graphics Press, Chesire, CT, 1987.
[34] J. S. Vitter and P. Flajolet.“Analysis of algorithms and data structures,”in Handbook of Theoretical Computer Science A:Algorithms and Complexity, J.van Leeuwen, ed., Elsevier, Amsterdam, 1990, 431-524.
[35] E. W. Weisstein, ed., MathWorld.
